Operator Learning Meets Numerical Analysis
Improving Neural Networks through Iterative Methods
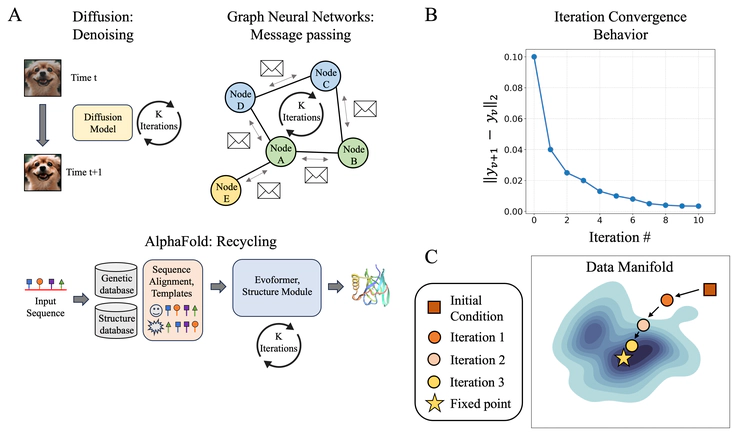Overview of iterative framework. (A) Popular architectures which incorporate iterative components in their framework. (B) Convergence behavior of an iterative solver. (C) Behavior of iterative solver converging to a fixed point in the data manifold.Abstract
Deep neural networks, despite their success in numerous applications, often function without established theoretical foundations. In this paper, we bridge this gap by drawing parallels between deep learning and classical numerical analysis. By framing neural networks as operators with fixed points representing desired solutions, we develop a theoretical framework grounded in iterative methods for operator equations. Under defined conditions, we present convergence proofs based on fixed point theory. We demonstrate that popular architectures, such as diffusion models and AlphaFold, inherently employ iterative operator learning. Empirical assessments highlight that performing iterations through network operators improves performance. We also introduce an iterative graph neural network, PIGN, that further demonstrates benefits of iterations. Our work aims to enhance the understanding of deep learning by merging insights from numerical analysis, potentially guiding the design of future networks with clearer theoretical underpinnings and improved performance.
Authors
- Emanuele Zappala
- Daniel Levine
- Sizhuang He
- Syed Rizvi
- Sacha Levy
- David van Dijk
Cite this paper
E. Zappala, D. Levine, S. He, S. Rizvi, S. L ́evy and D. van Dijk, Operator Learning Meets Numerical Analysis: Improving Neural Networks through Iterative Methods, arXiv:2310.01618